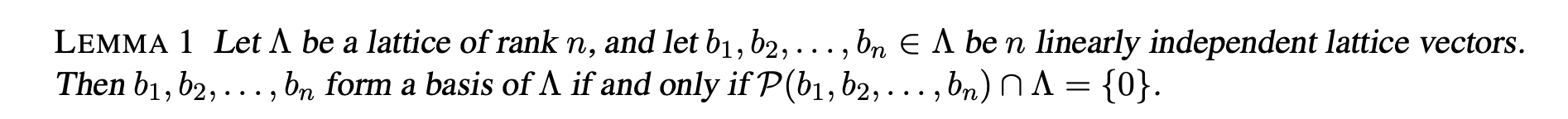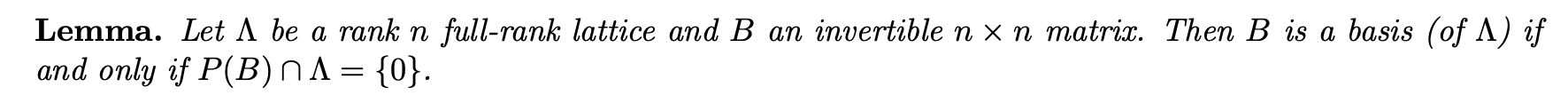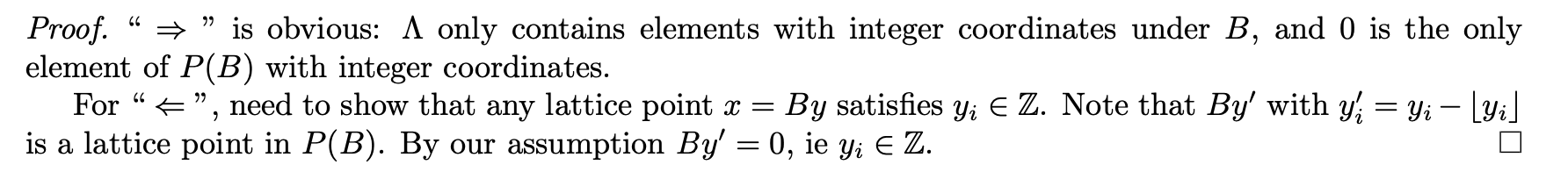FHE学习笔记 #5 格的基本概念
本文最后更新于:2022年11月16日 下午
CTF 中文百科:基本介绍 - CTF Wiki (ctf-wiki.org)
阮行止大佬的博客:格密码笔记(四) (ruanx.net)
其参考教程为:Hoffstein2015 Introduction to Mathematical Cryptography.pdf (emu.edu.tr)
纽约大学的课程:Lattices in Computer Science (Fall 2009) (nyu.edu)
MIT 的 LaTeX 教程(借鉴纽约大学的教程,但是貌似存在错误,下文会进行讨论,不需要参考):Lattices, fundamental parallelepiped and dual of a lattice, shortest vectors, Blichfield's theorem (mit.edu)
MIT 新教程 6.876J Advanced Topics in Cryptography (Fall 2015) (mit.edu)
文章使用 wolai 编写并导出,在 wolai 中观看效果更好,有颜色高亮和实时更新
基本概念
格 \(\Lambda\) 是 \(\mathbb R^n\) 对加法构成的一个离散子群(discrete additive subgroup of \(\mathbb R^n\))
\(B=\left(\mathbf{b}_{1}, \ldots, \mathbf{b}_{n}\right)\) 是 \(\mathbb R^m(n\le m)\) 上线性无关的向量组
格 \(\Lambda=\mathcal{L}(B)\) 就是由 \(B\) 中向量的整系数线性组合生成的,形式如下:
\[ \Lambda=\mathcal{L}(B)=\left\{\sum_{i=1}^{n} \gamma_{i} \mathbf{b}_{i}: \quad \gamma_{i} \in \mathbb{Z}, \mathbf{b}_{i} \in B\right\} \]
可以看出格和线性空间非常相似,区别在于格的线性组合系数为整数,突出格具有规整的特点,而线性空间的系数为任意实数。
\(\mathbb Z^n\) 就是 \(\mathbb R^n\) 上的格。
还有上面提到的离散子群,有个严谨的定义:
一个加法子群 \(L\) 是离散的,当且仅当存在一个常数 \(\epsilon>0\),使得下式成立:
\[ \forall \boldsymbol v \in L, \quad L \cap\left\{\boldsymbol{w} \in \mathbb{R}^{m}:\|\boldsymbol{v}-\boldsymbol{w}\|_2<\epsilon\right\}=\{\boldsymbol{v}\} \]
几何意义:对于 \(L\) 中的任意向量 \(\boldsymbol v\),其附近 \(\epsilon\) 的(欧几里得)距离范围内,不存在 \(L\) 的其他向量。
人话版本:任意两个向量之间的距离都不小于某个(足够小的)常数。
正因为有整数系数的限制,才能实现离散。
类似线性空间,\(B\) 称为格 \(\mathcal{L}(B)\) 的基,同时任意一个可以生成 \(\mathcal{L}(B)\) 的向量组都是它的基,同一个格的基所含向量个数相同。
非零子空间 \(H\) 的维数(用 \(\operatorname{dim} H\) 表示)是 \(H\) 的任意一组基中向量的个数。
有分歧的一点是格的维数 dimension:
有的教材说 \(n\) 个向量生成的格的维数应该是 \(n\),但是也有教材说是 \(m\)。
同理格 \(\mathcal{L}(B)\) 的秩 rank 为 \(n\),这点没有争议。
当 \(n=m\) 时,称格 \(\mathcal{L}(B)\) 是满秩 full-rank 的。
格的生成空间 Span of Lattice:
其实就是格基的线性生成空间,形式为:
\[ \operatorname{span}(\mathcal{L}(B))=\operatorname{span}(B)=\left\{B y \mid y \in \mathbb{R}^{n}\right\} \]
格的基本域 Fundamental Domain
通常也叫格的 Fundamental Parallelepiped,它的形式为:
\[ \mathcal{P}(B)=\left\{B x \mid x \in [0,1)^n\right\}=\left\{\sum_{i=1}^{k} x_{i} \mathbf{b}_{i}: \quad x_{i} \in[0,1)\right\} \]
也有说 \(x_i\in[-1 / 2,1 / 2)\) 的,但是下文的定理都使用 \(x_i\in[0,1 )\) 这种形式)
下图是格 \(\mathbb Z^2\) 的基本域的例子:
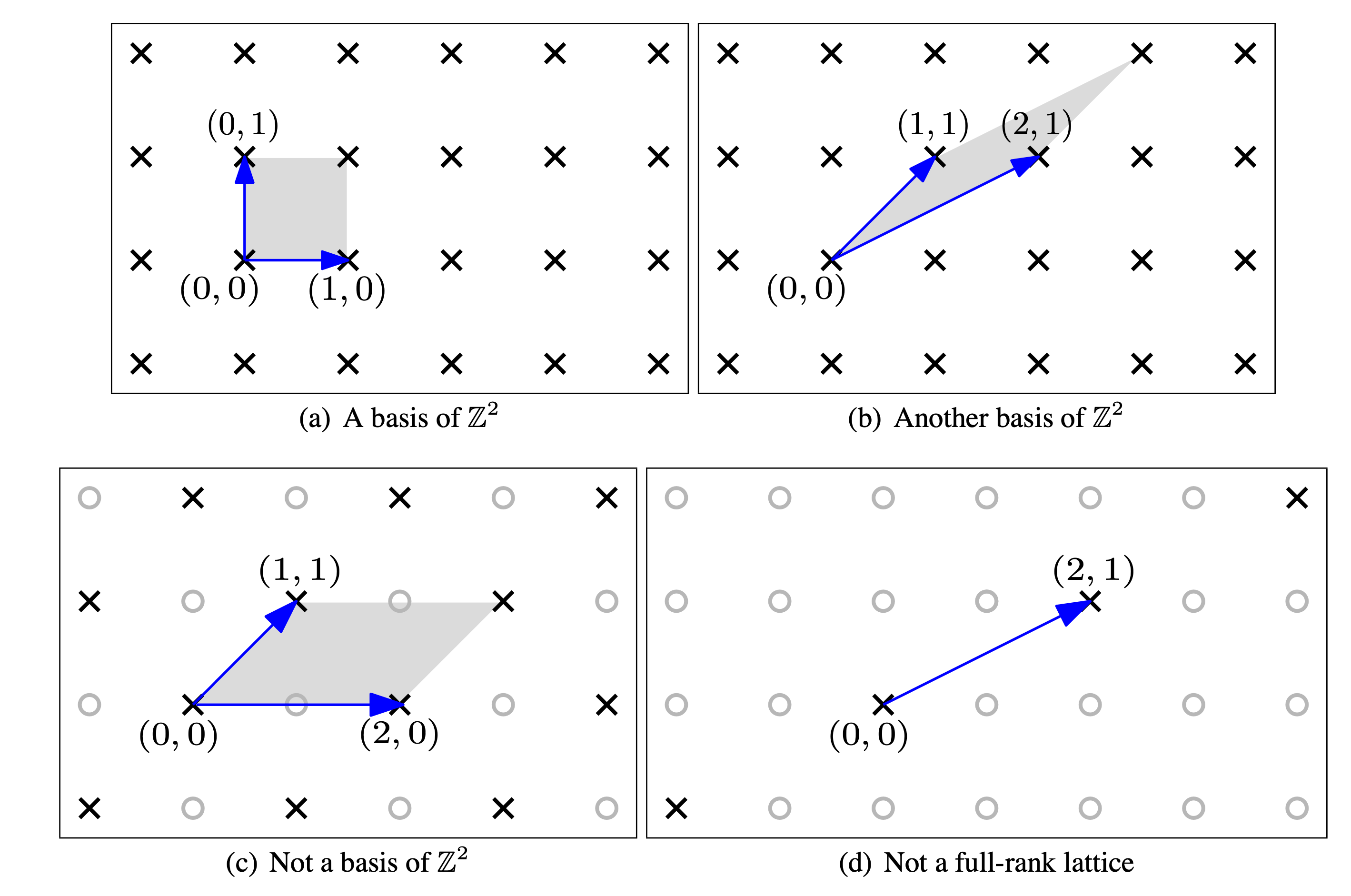
值得注意的点:
- 和 (b) 都是 \(\mathbb Z^2\) 的基,灰色区域是它们生成的基本域,注意 (a) 的基本域是不包含点 (0, 1), (1, 0), (1, 1) 的,只包含了唯一一个整点 (0, 0),同样的 (b) 也是只包含一个整点 (0, 0)
- 之所以不是基,是因为它无法通过整系数线性组合表示 (1, 0) 等点,而它的基本域却包含了 (1, 0),这其实隐藏了一个判断基的标准,后续会详细证明
- 所含向量个数为 1,秩为 1,很明显不能生成格 \(\mathbb Z^2\)
基本域 \(\mathcal{P}(B)\) 和格基的线性生成空间 \(\text{span}(B)\) 存在一定的关系:
当把基本域 \(\mathcal{P}(B)\) 复制到 \(\mathcal{L}(B)\) 的每个格点上时,就会形成 \(\text{span}(B)\) 的一种平铺 tiling,像铺瓷砖一样。
将例子 (b) 中的基本域进行复制,得到如图所示的平铺:

这其实暗含了一个定理:
\(\mathcal{L}(B)\) 是 \(\mathbb R^n\) 上的满秩格,任意 \(\boldsymbol{w} \in \mathbb{R}^{n}\) 都能表示为一个基本域 \(\mathcal{P}(B)\) 中向量和一个 \(\mathcal{L}(B)\) 中向量的和的形式,且是唯一确定的,即:
\[ \boldsymbol{w}=\boldsymbol{t}+\boldsymbol{v} \quad \text{for}\; \text{a}\; \text{unique} \;\boldsymbol{t} \in \mathcal{P}(B)\; \text{and}\; \text{a}\; \text{unique}\; \boldsymbol{v} \in \mathcal{L}(B) \]
也就是 \(\mathcal{P}(B)+\boldsymbol{v}=\{\boldsymbol{t}+\boldsymbol{v}: \boldsymbol{t} \in \mathcal{P}(B)\},\boldsymbol{v} \in \mathcal{L}(B)\) 可以覆盖整个 \(\mathbb R^n\)

在介绍完基本域后,就可以判定 \(\mathbb R^n\)上的基到底是不是格基了。从之前的例子可以看出,线性无关的向量组并不一定是格的基,而区别就在于基本域的覆盖范围是不是只包含格中的零点。
引理:\(\Lambda\) 是 \(\mathbb R^n\) 上的满秩格,\(B=\left(\boldsymbol{b}_{1}, \ldots, \boldsymbol{b}_{n}\right),\boldsymbol{b_1},\boldsymbol{b_2},\ldots,\boldsymbol{b_n}\in\mathcal \Lambda\),且为 \(n\) 个线性无关的向量。那么 \(B\) 是 \(\Lambda\) 的基 \(\iff\) \(\mathcal P(B)\cap \Lambda=\{\boldsymbol 0\}\)
证明:
先证 \(\Rightarrow\):
\(B=\left(\boldsymbol{b}_{1}, \ldots, \boldsymbol{b}_{n}\right)\) 是格 \(\Lambda\) 的基
基本域 \(\mathcal P(B)\) 的线性组合系数都是 \([0,1)\) 中的实数,而在格 \(\Lambda\) 中,\(B\) 的线性组合系数是所有整数
因为这两个线性组合所使用的向量组都是相同的,且向量组是线性无关的,即格上的每个向量的线性表示是唯一的
而这两个线性组合的系数唯一交集就是 0,则线性组合的交集只有零向量,即 \(\mathcal P(B)\cap \Lambda=\{\boldsymbol 0\}\)
再证 \(\Leftarrow\):
\(B=\left(\boldsymbol{b}_{1}, \ldots, \boldsymbol{b}_{n}\right),\mathcal P(B)\cap \mathcal \Lambda=\{\boldsymbol 0\}\),且为格 \(\Lambda\) 上 \(n\) 个线性无关的向量,所以可以作为 \(\mathbb R^n\) 上的一组基
对于任意 \(\boldsymbol x\in \Lambda\),都可以由 \(B\) 线性表示为 \(\boldsymbol x=B\boldsymbol y=\sum_{i=1}^n b_i y_i,y_i\in\mathbb R\)
记 \(\lfloor \boldsymbol y\rfloor=(\lfloor y_1\rfloor,\lfloor y_2\rfloor,\ldots,\lfloor y_n\rfloor)^T\),可以发现 \(\boldsymbol y'=\boldsymbol y-\lfloor\boldsymbol y\rfloor\) 满足 \(y'_i\in[0,1)\),所以 \(B\boldsymbol y'\in \mathcal P(B)\)
如果我们能证明 \(B\boldsymbol y'\) 也是格 \(\Lambda\) 上的向量,利用 \(\mathcal P(B)\cap \Lambda=\{\boldsymbol 0\}\) 就能证明 \(\boldsymbol y'\) 为零向量,即 \(\boldsymbol y\) 中元素都是整数。
因为 \(B\) 中的向量都在格 \(\Lambda\) 上,所以 \(B\lfloor\boldsymbol y\rfloor\) 也在格上(因为是对加法封闭的群),又因为 \(\boldsymbol x=B\boldsymbol y\) 本来就在格上,所以 \(B\boldsymbol y-B\lfloor\boldsymbol y\rfloor=B\boldsymbol y'\) 也在格上
利用 \(\mathcal P(B)\cap \Lambda=\{\boldsymbol 0\}\) 得知 \(\boldsymbol y'=\boldsymbol 0\),即 \(\boldsymbol y\) 中元素都是整数,所以任意 \(\boldsymbol x\in\Lambda\),都可以用 \(B\) 整数系数线性表示,故 \(B\) 就是格 \(\Lambda\) 的基。
这里贴出纽约大学和 MIT 的教材中关于这个引理的描述:
可以看到 MIT 的 \(B\) 的定义和格没有关系,这就会导致证明 \(\Leftarrow\) 时条件不足,无法证明 \(B\boldsymbol y'\) 也是格上的向量
这是 MIT 的证明过程:
笔者思考了很久,也没有想明白为什么 \(B\boldsymbol y'\) 也是格上的向量,后面通过查找其参考的文献作者,搜到了纽约大学的原文才发现端倪。
如果有其他看法,欢迎来讨论
格的行列式 Determinant
可能翻译成「行列式」不太正确
\(\Lambda=\mathcal{L}(B)\) 是 \(n\) 维格,记它的行列式为 \(\operatorname{det}(\Lambda)\),也称为基本域 \(\mathcal P(B)\) 的 \(n\) 维体积 volume,记为 \(\operatorname{Vol}(\Lambda)\)。形式化表示为 \(\operatorname{det}(\Lambda):=\sqrt{\operatorname{det}\left(B^{T} B\right)}\)。
当 \(\Lambda\) 是满秩格时,\(B\) 是个方阵, 有特殊形式 \(\operatorname{det}(\Lambda)=|\operatorname{det}(B)|\)。
格行列式的大小和它的密度成反比
Hadamard 不等式:
\(B=\left(\mathbf{b}_{1}, \ldots, \mathbf{b}_{n}\right)\) 是格 \(\Lambda\) 的基,其基本域为 \(\mathcal P(B)\),则下述不等式成立:
\[ \operatorname{det} (\Lambda)=\operatorname{Vol}(\mathcal{P}(B)) \leq\left\|\boldsymbol{b}_{1}\right\|\left\|\boldsymbol{b}_{2}\right\| \cdots\left\|\boldsymbol{b}_{n}\right\| \]
格和幺模矩阵 Unimodular Matrix
幺模矩阵是 \(\mathbb Z^{n\times n}\) 上的方阵,其行列式值为 \(+1\) 或 \(-1\)。
幺模矩阵的一些性质:
\(\mathbb Z^{n\times n}\) 上的幺模矩阵关于矩阵乘法构成 \(\mathbb Z\) 上的一般线性群 General Linear Group,表示为 \(\mathrm{GL}_{n}(\mathbb{Z})\)
\(n\) 阶的一般线性群由 \(n\times n\) 的可逆矩阵构成,它们关于一般的矩阵乘法构成一个群。这是因为两个可逆矩阵的乘积仍为可逆矩阵。
而两个幺模矩阵的乘积仍为幺模矩阵,且幺模矩阵的逆也是幺模矩阵,神奇的是元素均为整数。
引理:\(B_{1}, B_{2} \in \mathbb{R}^{m \times n}\) 且列向量线性无关,由他们生成的格相同 \(\iff\)存在幺模矩阵 \(U\) 使得 \(B_2=B_1U\) 成立。
证明:
先证 \(\Rightarrow\):
设 \(B_1,B_2\) 都是格 \(\mathcal L\) 的基,即 \(\mathcal{L}\left(B_{1}\right)=\mathcal{L}\left(B_{2}\right)\)
因为基中的列向量也是格上的向量,所以 \(B_2\) 中的列向量 \(\boldsymbol b_i\) 都可以表示为 \(\boldsymbol b_i=B_1\boldsymbol y_i, \boldsymbol y_i\in \mathbb Z^n\)的形式,即:
\[ \begin{aligned} B_2&=[\boldsymbol b_1,\boldsymbol b_2,\ldots,\boldsymbol b_n]=B_1[\boldsymbol y_1,\boldsymbol y_2,\ldots,\boldsymbol y_n],\quad\boldsymbol y_i\in \mathbb Z^n\\ &=B_1U,\quad U\in\mathbb Z^{n\times n} \end{aligned} \]
同理,有 \(B_1=B_2V, V\in\mathbb Z^{n\times n}\)
综上,得到 \(B_{2}=B_{1} U=B_{2} V U\),为了凑出方阵计算行列式,使用下式:
\[ B_{2}^{T} B_{2}=(V U)^{T} B_{2}^{T} B_{2}(V U) \]
取行列式,得到 \(\operatorname{det}\left(B_{2}{ }^{T} B_{2}\right)=(\operatorname{det}(V U))^{2} \operatorname{det}\left(B_{2}{ }^{T} B_{2}\right)\),整理得到: \(\operatorname{det}(V) \operatorname{det}(U)=\pm1\)
又因为 \(U,V\in\mathbb Z^{n\times n}\),它们的行列式也是整数,所以 \(\operatorname{det}(U)=\pm 1\),即存在幺模矩阵 \(U\) 使得 \(B_2=B_1U\) 成立
再证 \(\Leftarrow\):
\(B_2=B_1U\) 对于某个幺模矩阵 \(U\) 成立
任意 \(\mathcal L(B_2)\) 上的向量 \(\boldsymbol x\) 都可以表示为 \(\boldsymbol x=B_2\boldsymbol y,\boldsymbol y\in \mathbb Z^n\) 的形式,代入 1 中可得 \(\boldsymbol x=B_1U\boldsymbol y,\boldsymbol y\in \mathbb Z^n\)
因为 \(U\boldsymbol y\in\mathbb Z^n\),所以有 \(\mathcal{L}\left(B_{2}\right) \subseteq \mathcal{L}\left(B_{1}\right)\),因为任意 \(\mathcal L(B_2)\) 上的向量都可以被 \(B_1\) 的整系数线性组合表示
同理,\(B_1=B_2U^{-1}\),而幺模矩阵的逆仍为幺模矩阵,所以 \(\mathcal{L}\left(B_{1}\right) \subseteq \mathcal{L}\left(B_{2}\right)\)
综上所述,有 \(\mathcal{L}\left(B_{1}\right)=\mathcal{L}\left(B_{2}\right)\),即 \(B_1,B_2\) 生成的格相同
对偶格 Dual Lattice
也叫 Reciprocal Lattice
格 \(\Lambda\) 的对偶格记为 \(\Lambda^*\),形式为:
\[ \Lambda^{*}=\{\boldsymbol y \in \operatorname{span}(\Lambda) \mid \forall\boldsymbol x \in \Lambda,\langle\boldsymbol x,\boldsymbol y\rangle \in \mathbb{Z}\} \]
\(\Lambda^*\) 也是一个格,其上的向量和格 \(\Lambda\) 的向量内积都为整数
\((\mathbb Z^n)^*=\mathbb Z^n\),也叫自对偶 Self-dual 格。
类似的,\(\left(2 \mathbb{Z}^{n}\right)^{*}=\frac{1}{2} \mathbb{Z}^{n}\),这也很好理解,因为 \(2\mathbb Z^n\)中都是偶数,乘上任意 \(\frac{1}{2} \mathbb{Z}^{n}\) 中的数都能得到整数。
这样通过倒数得到对偶格的方式,其实就是它被称为 Reciprocal Lattice 的原因。
对偶格中的向量可以给原格中的向量进行分层,得到一系列超平面 Hyperplanes Perpendicular:
取对偶格 \(\Lambda^*\) 中的向量 \(\boldsymbol x\),将 \(\Lambda\) 所有与它内积结果相同的向量划分到同一层。下面是长短两个向量的分层情况。红色是对偶格中的向量点,黑色是原来格中的点。
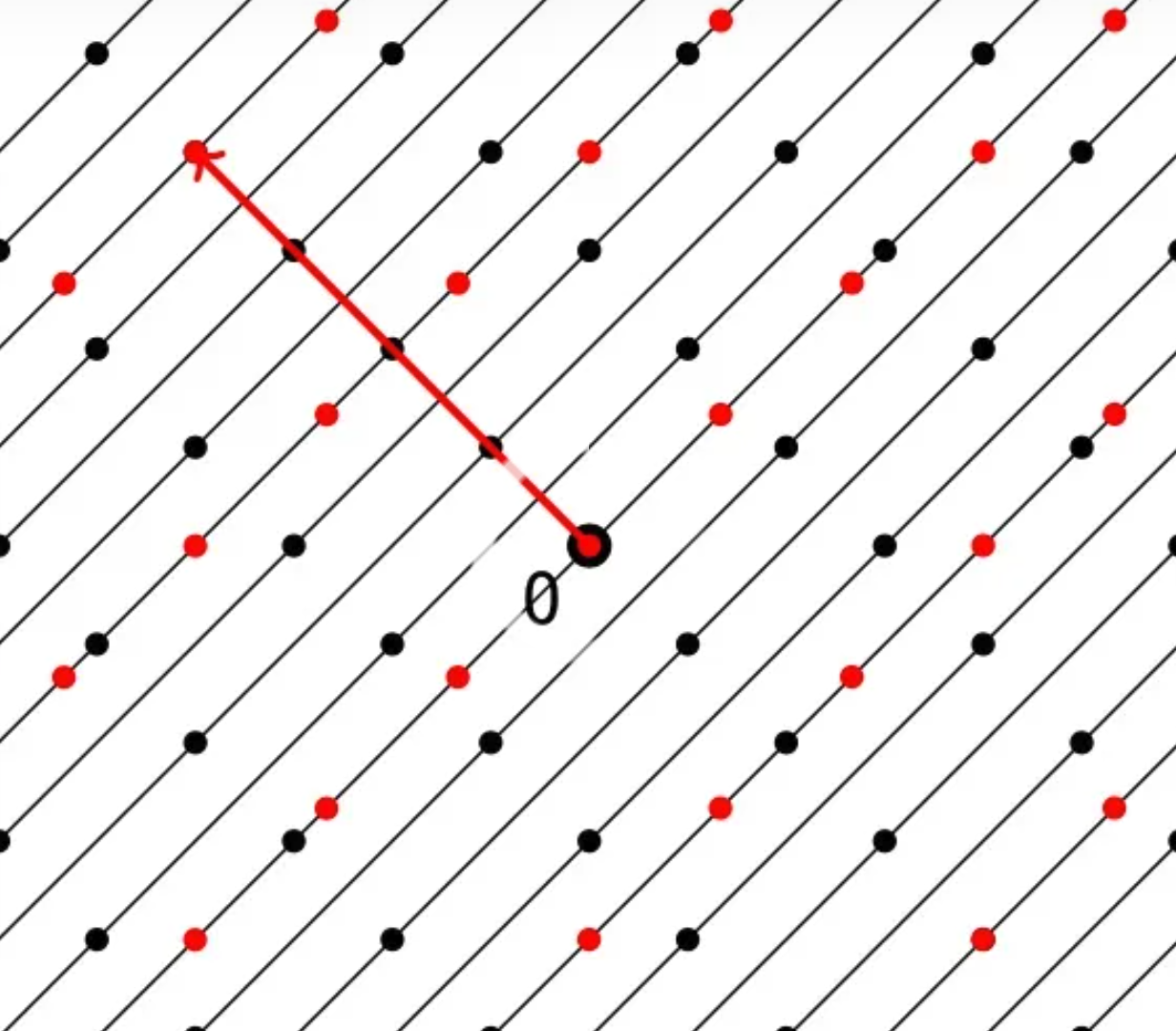
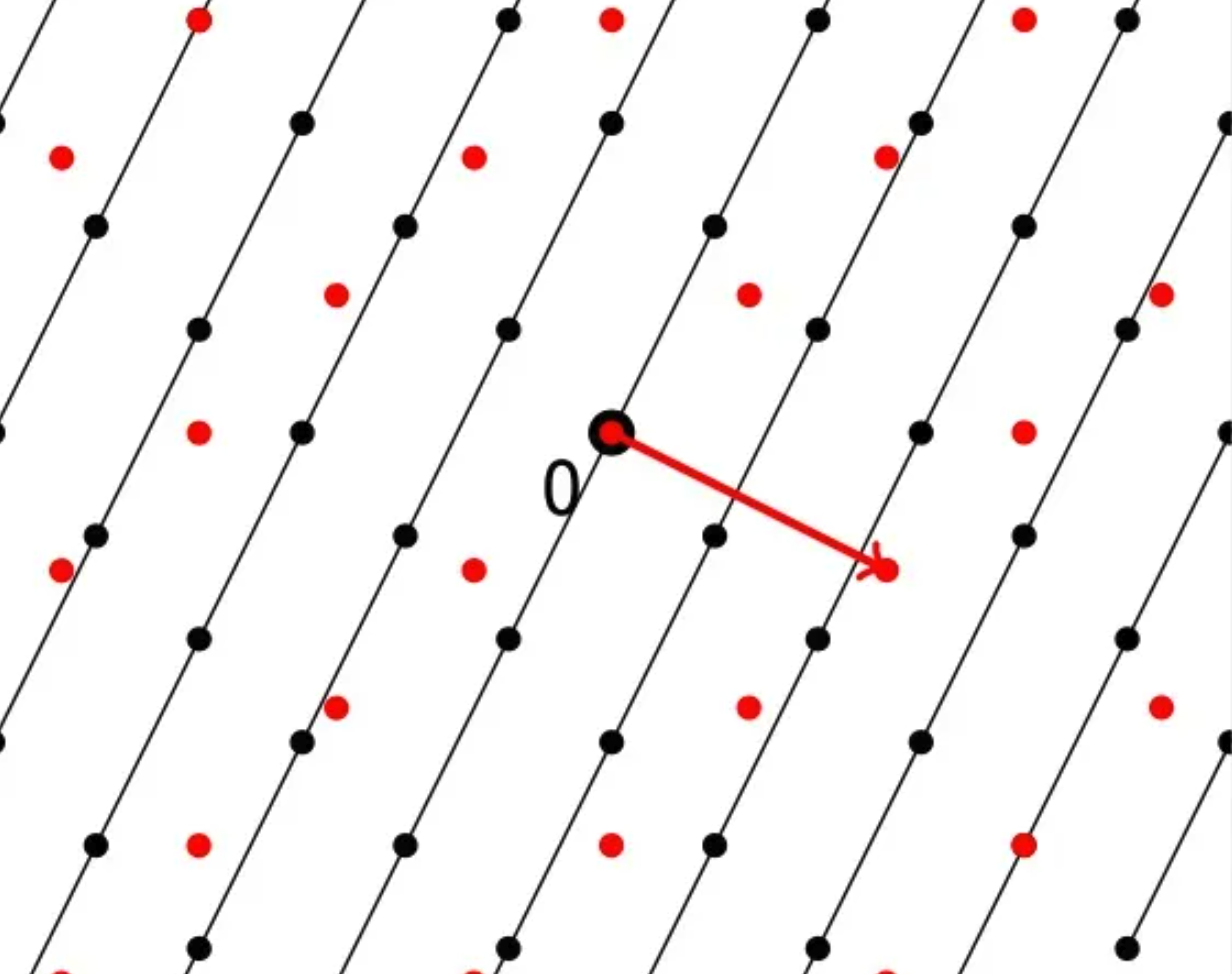
层之间的距离为 \(\frac{1}{\|\boldsymbol x\|}\),也就是选的向量越长,层之间的距离越小
可以用来逼近格的覆盖半径
https://sysmath.com/jweb_xtkxysx/CN/10.12341/jssms11935#1
格 \(\Lambda\) 的覆盖半径是指每个格点为圆心作球时,能覆盖住 \(\text{span}(\Lambda)\) 的最小半径,也就是 \(\text{span}(\Lambda)\) 中点到格点的最远距离。
因为层与层之间没有任何格点,所以当选取较短的向量时,就可以用层间距来近似覆盖半径
一些引理:
对偶格的对偶等于原格,即 \(\left(\Lambda^{*}\right)^{*}=\Lambda\)
\(\operatorname{det}\left(\Lambda^{*}\right)=1 / \operatorname{det}(\Lambda)\)
对偶格基 Dual Basis
定义:
格 \(\Lambda\) 的基为 \(B=\left(b_{1}, \ldots, b_{n}\right) \in \mathbb{R}^{m \times n}\),则其对偶格基记为 \(D=\left(d_{1}, \ldots, d_{n}\right) \in \mathbb{R}^{m \times n}\),同时 \(D\) 是唯一满足下述条件的基:
\(\operatorname{span}(D)=\operatorname{span}(B)\)
\(B^{T} D=I\)
更直观的表示为: \(\left\langle b_{i}, d_{j}\right\rangle=\delta_{i j}\),只有当 \(i=j\) 时 \(\delta_{i j}=1\),其余情况均为 0。
当 \(\Lambda\) 为满秩格时,对偶格基为 \(D=\left(B^{T}\right)^{-1}\) ;一般情况下,对偶格基为 \(D=B\left(B^{T} B\right)^{-1}\)。
对偶基可以证明对偶格确实为一个格:
如果 \(D\) 是 \(B\) 的对偶基,那么 \((\mathcal{L}(B))^{*}=\mathcal{L}(D)\),即对偶格就是由对偶基生成的格。
证明:
先证 \(\mathcal{L}(D)\subseteq (\mathcal{L}(B))^{*}\):
任意 \(\mathcal L(B)\) 中的向量 \(\boldsymbol x\) 都能写成 \(\boldsymbol x=\sum a_{i} \boldsymbol b_{i},a_i\in\mathbb Z\) 的形式
任意对偶格基中的向量 \(\boldsymbol d_j\) 和 \(\boldsymbol x\) 的内积为:
\[ \left\langle \boldsymbol x, \boldsymbol d_{j}\right\rangle=\sum a_{i}\left\langle\boldsymbol b_{i},\boldsymbol d_{j}\right\rangle=a_{j} \in \mathbb{Z} \]
所以对偶格基中的向量都包含在对偶格 $ ((B))^{*} $
又因为对偶格中的向量加法满足封闭性,所以 \(D\) 生成的格也都包含在对偶格 $ ((B))^{*} $中,得证
再证 \((\mathcal{L}(B))^{*}\subseteq \mathcal{L}(D)\):
任意 \(\boldsymbol y\in (\mathcal{L}(B))^{*}\),根据对偶格和对偶格基的定义,有 \(\boldsymbol y \in \operatorname{span}(B)=\operatorname{span}(D)\),所以 \(\boldsymbol y\) 可以写成 \(\boldsymbol y=\sum a_{i} \boldsymbol d_{i}, a_i\in\mathbb R\) 的形式
只要证明 \(a_i\) 其实都是整数就能证明 \(\boldsymbol y\in \mathcal L(D)\)
使用格基 \(B\) 中的向量 \(\boldsymbol b_j\) 和 \(\boldsymbol y\) 作内积,因为 \(\boldsymbol y\) 是对偶格中的向量,内积结果是整数:
\[ \mathbb{Z} \ni\left\langle\boldsymbol y,\boldsymbol b_{j}\right\rangle=\sum a_{i}\left\langle\boldsymbol d_{i},\boldsymbol b_{j}\right\rangle=a_{j} \]
因为 \(\boldsymbol y=\sum a_{i} \boldsymbol d_{i}, a_i\in\mathbb Z\),所以 \(\boldsymbol y\in \mathcal L(D)\),也就证明了 \((\mathcal{L}(B))^{*}\subseteq \mathcal{L}(D)\)。