FHE学习笔记 #2 多项式环
本文最后更新于:2022年11月16日 下午
https://en.wikipedia.org/wiki/Polynomial_ring
环论(4/5/上): 一元多项式的基本理论 - 知乎 (zhihu.com)
这篇知乎文章讲的比较透彻,但是不易理解,可以结合以下视频学习。
无尽沙砾大佬的视频:3-6-多项式环-4_哔哩哔哩_bilibili ~ 3-6-多项式环-8_哔哩哔哩_bilibili
顾沛老师的视频:30.多项式环1_哔哩哔哩_bilibili
本文主要是简化了知乎文章的叙述,优化了公式的显示效果,便于自己理解
文章使用 wolai 编写并导出,在 wolai 中观看效果更好,有颜色高亮和实时更新
背景
以往认知中的多项式是函数形式的,且定义在数域上。如果 \(\mathbb{P}\) 是 一个数域,那么 \(\mathbb{P}\) 上的一元多项式环 \(\mathbb{P}[x]\) 是由形如
\[ a_n x^n+a_{n-1} x^{n-1}+\cdots+a_1 x+a_0, \quad n \geqslant 0, \quad a_i \in \mathbb{P}, \quad i=0,1, \ldots, n \]
的元素组成的集合。集合 \(\mathbb{P}[x]\) 上两个元素 \(a_n x^n+a_{n-1} x^{n-1}+\cdots+a_1 x+a_0, b_m x^m+b_{m-1} x^{m-1}+\cdots+b_1 x+b_0\)(不妨设 \(m \geqslant n\))相等当且仅当对任何 \(0 \leqslant i \leqslant m, a_i=b_i\)(这里规定,如果 \(k>n\),则 \(a_k=0\))。而环 \(\mathbb{P}[x]\) 的加法就是合并同类项,乘法是展开相乘再合并同类项。
但是实际上多项式可以推广到一般环上,这样的定义会出问题。例如 \(x\) 究竟是什么东西,取值是什么,它可能都不需要取自数域 \(\mathbb{P}\)。所以必须更严格的给出 \(x\) 的定义,其实就是后面所谓的超越元(不定元)。
$ R $ 上添加 \(u\) 形成的环 \(R[u]\)
为了和知乎大佬、顾沛老师的记号统一,用 \(u\) 来表示之前认知中的 \(x\),也就是自变量。
多项式的系数是定义在一个环 \(R\) 上的,若 \(R\) 和 \(u\) 要组成多项式运算,则要求他们的运算结果在一个更大的环 \(R[u]\) 上,且要求这是包含 $ R{u} $ 最小的环。
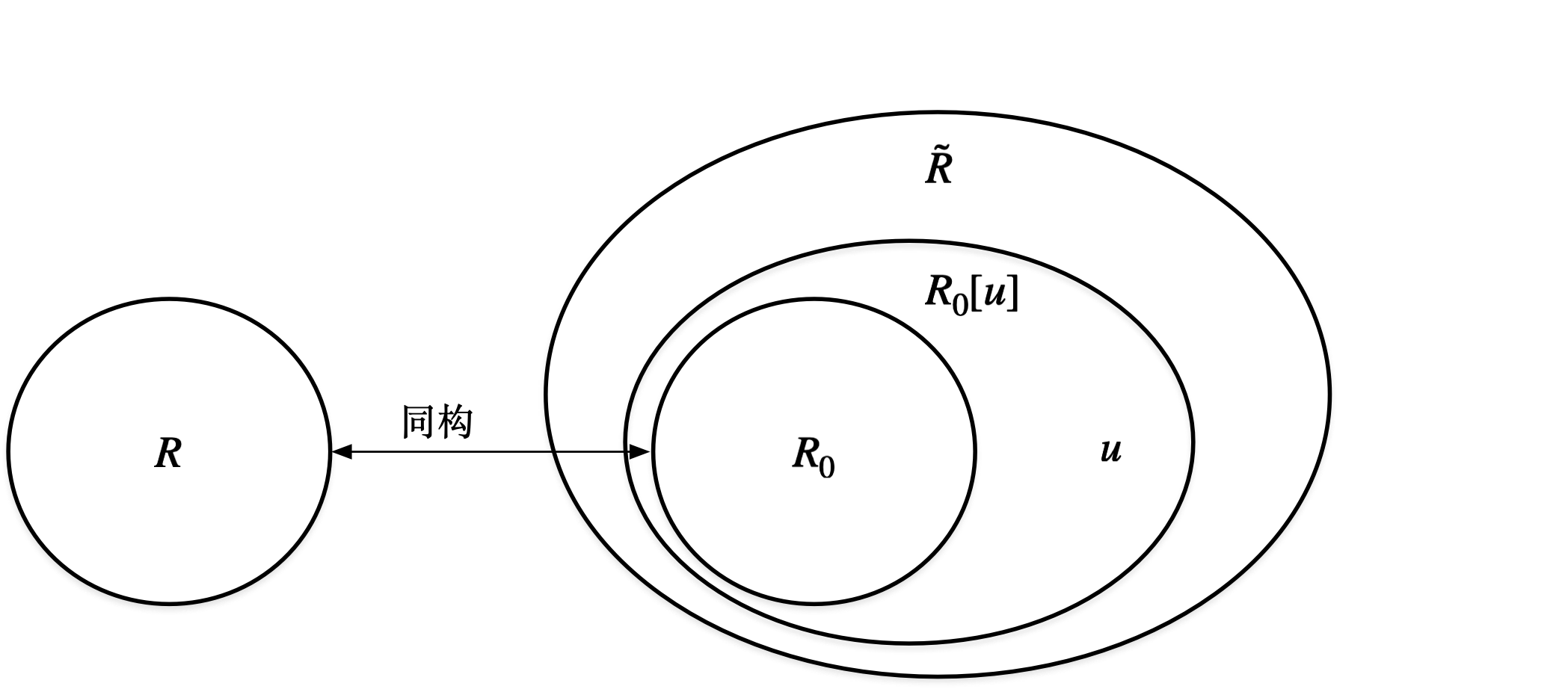
这里有一个更大的环 \(\widetilde R\),它包含了 \(R,u,R[u]\),至于为什么有这个环笔者也不太清楚 🥲
他们之间的关系是这样的:
为了构造出环 \(R[u]\),考虑它里面的每个元素 \(x\),都是由以下几种形式构成:
\(R\) 中的元素,即 \(x \in R\),且它们之间的乘法加法都是封闭的,都在 \(R\) 中
\(u\) 的自乘,即存在某个正整数 \(n\) 使得 \(x=u^n\)
\(u\) 的自加,即存在某个整数 \(m\) 使得 \(x=m u\)
\(u\) 的自乘和 \(R\) 中元素的互乘,即存在 \(a, b \in R\) 和正整数 \(n\) 使得 \(x=a u^n\) 或 \(x=u^n a\) 或 \(x=a u^n b\)
上述情况的加和,\(x=r+\sum_n m_n u^n+\sum_n a_n u^n+\sum_n u^n b_n+\sum_n c_n u^n d_n\),\(r \in R, a_n, b_n, c_n, d_n\) 是 \(R\) 当中的元素序列
这样 \(R[u]\) 的元素形式比较复杂,通常我们要求 \(R\) 和 \(\widetilde{R}\) 都是可换幺环,并且它们的幺元相同,来简化元素形式,同时更贴近多项式的形式。
在这样要求以后,我们看到 \(u^n\) 的自加 \(m u^n\) 可以表述为 \[ \sum_{i=1}^m u^n=\sum_{i=1}^m\left(1 u^n\right)=\left(\sum_{i=1}^m 1\right) u^n \]
因为 \(1 \in R\) 而 \(R\) 是环,因此 1 的自加也在 \(R\) 当中,即存在 \(a \in R\) 使得 \(\begin{aligned}a=\sum_{i=1}^m 1\end{aligned}\),进而自加 \(m u^n\) 可以表示为 \(a u^n, a \in R\) 的形式,同理自乘也可以化成 \(a u^n, a \in R\) 的形式。其余可以通过交换性获得相同的形式。最后 \(R[u]\) 中元素的形式简化为:
\[ x=a_0+\sum_n a_n u^n, a_0, a_n \in R \]
可以人为规定 \(u^0=1\),最后将其写成 \(x=\sum_n a_n u^n , n\) 取值从0开始,到某个正整数。
这样可以得到「交换幺环上添加元素得到的环」的定义:
设 \(R\) 是交换环,\(\widetilde R\) 是它的扩环,\(u \in \widetilde R \backslash R\),则称
\[ R[u]:=\left\{\sum_{i=0}^n a_i u^i \mid n \in \mathbb{N}, a_i \in R\right\} \]
为在 \(R\) 中添加元素 \(u\) 所得到的环,称 \(a_i u^i\) 为 \(R[u]\) 中某个元素的项,\(a_i\) 为这一项的系数 coefficient。
在更一般的定义当中,我们其实不强制要求 \(u \in \widetilde{R} \backslash R\),不过这种情况下和 \(R[u]=R\),同时 \(u\) 不是超越元,我们这里的定义希望排除这种情况。
可以证明 \(R[u]\) 就是包含 $ R{u} $ 最小的环。
代数元 Algebraic Element 和超越元 Transcendental Element
我们如果将 \(R[u]\) 当中的 \(u^0(=1), u, u^2, \ldots, u^n, \ldots\) 视作是一些向量,那么 \(R[u]\) 当中的元素 \(\begin{aligned}\sum_{i=0}^n a_i u^i\end{aligned}\) 就可以视作是这些向量的「线性组合」。仿照线性代数当中的说法,我们可以引入代数元和超越元的定义:
设可换幺环 \(R\) 是可换幺环 \(\widetilde{R}\) 的子环,且它们拥有相同的么元,\(u \in \widetilde{R}\) 若存在 \(R\) 中的元素 \(\left\{a_i\right\}_{i=0}^n\)(其中至少某个 \(a_i \neq 0\))使得 \(\begin{aligned}\sum_{i=0}^n a_i u^i=0\end{aligned}\),则称 \(u\) 是 \(R\) 上的代数元,否则称其为 \(R\) 上的超越元。
从定义中即可看到,\(u \in R\) 必然是代数元,因为我们总是可以取 \(a_0=-u, a_1=1\) 使得 \(a_0+a_1 u=0\)。
因此在讨论代数元与超越元的时候,我们通常只是在 \(\widetilde{R} \backslash R\) 当中考虑。
在 \(R\) 上可以通过添加代数元或超越元可以生成环 \(R[u]\)。
如果借用前文所述「线性相关」的说法,可以看到:
\(u\) 是超越元:对于任意的 \(n\),\(u^0, \ldots, u^n\) 都是「线性无关」的
\(u\) 是代数元:对某个 \(n\),\(u^0, u, \ldots, u^n\) 是「线性相关」的
对于代数元 \(u\),可以额外引入其次数 Degree 的概念,符号为 \(\operatorname{deg}(u, R)\),定义如下:
\[ \begin{gathered} \operatorname{deg}(u, R):=\min \left\{n \in \mathbb{N}\mid \exists\{a_i\}_{i=0}^n \subseteq R \text { s.t. } \sum_{i=0}^n a_i u^i=0 \wedge \exists m\in \mathbb{N}(0 \leq m \leq n, a_m \neq 0)\right\} \end{gathered} \]
人话版本就是找到一个最小的自然数 \(n\),使得一个系数不全为 0 的多项式 \(\begin{aligned}\sum_{i=0}^n a_i u^i=0\end{aligned}\)。
另一种等价表示是:
\[ \begin{gathered} \operatorname{deg}(u, R):=\min \left\{n \in \mathbb{N}\mid \exists\{a_i\}_{i=0}^n \subseteq R \text { s.t. } \sum_{i=0}^n a_i u^i=0 \wedge a^n\not=0\right\} \end{gathered} \]
其实只要要求最后一个 \(a^n\not=0\) 即可,因为如果 \(a^n=0\wedge\exists i\in[0,n-1],a^i\not=0\) 使得 \(\begin{aligned}\sum_{i=0}^n a_i u^i=0\end{aligned}\),那么系数应该至多为 \(i\) 才对,而不是 \(n\)。
例子:
\(\operatorname{deg}(\sqrt{-1}, \mathbb Z)=\operatorname{deg}(\sqrt{-1}, \mathbb Q)=2\),因为没有实数 \(a_0,a_1\) 可以使得 \(a_0+a_1\times\sqrt{-1}=0\),而 \(1+0\times\sqrt{-1}+1\times(\sqrt{-1})^2=0\)
\(\operatorname{deg}(\sqrt{-1}, \mathbb C)=1\),在复数域上可以取 \(1,\sqrt{-1}\),使得 \(1+(\sqrt{-1})\times(\sqrt{-1})=0\)
一元多项式环和一元多项式
有了上述铺垫之后,我们就可以定义一元多项式了:
设 \(u\) 是可换幺环 \(R\) 上的超越元(不定元),则称 \(R[u]\) 为 \(R\) 上的一元多项式环,它里面的元素被叫做一元多项式,记为 \(f(u)=\begin{aligned}\sum_{i=0}^n a_i u^i=0\end{aligned}\)。
次数最高项系数为 1 的多项式称为首一多项式 Monic Polynomial
我们之所以要求 \(u\) 是不定元, 主要是因为我们希望得到下面的一个结论:
设 \(R[u]\) 是交换么环 \(R\) 上的一元多项式环,\(\begin{aligned}f_1(u)=\sum_{i=0}^n a_i u^i\end{aligned}\) 和 \(\begin{aligned}f_2(u)=\sum_{i=0}^m b_i u^i\end{aligned}\),则 \(f_1(u)=f_2(u)\) 当且仅当:
\(a_i=b_i\) 对任意 \(i, 0 \leq i \leq \min (m, n)\) 成立
当 \(i>\min (m, n)\) 之后必须恒有 \(a_i=0\)(如果 \(n>m\))或 \(b_i=0\)(如果 \(m>n\))
根据不定元的性质进行证明:
不妨设 \(m \leq n\), 则 \(f_1(u)=f_2(u)\iff f_1(u)-f_2(u)=0\), 这就等价于
\[ \sum_{i=0}^m\left(a_i-b_i\right) u^i+\sum_{j=m+1}^n a_i u^j=0 \]
而根据不定元的要求,此时必须有
\[ \begin{aligned} a_i-b_i &=0,0 \leq i \leq m \\ a_i &=0, m+1 \leq i \leq n \end{aligned} \]
这就表明 \(p_1(u)\) 自 \(a_{m+1}\) 开始(包括它自身)后续的 \(a_i\) 都是零,且前面的 \(m+1\) 项恒有 \(a_i=b_i\)。
如果我们不对 \(u\) 做要求,就会使得多项式环中元素的多项式表示不唯一,两个多项式的相等关系就很难建立起来,给研究带来困难。
但是存在可换幺环没有不定元,此时多项式表示不唯一。
在定义中,每个多项式都可以写成 \(\begin{aligned}\sum_{i=0}^n a_i u^i\end{aligned}\) 的样子,这里的 \(n\) 是不固定的,所以上述定理中两个相等的多项式可以相差任意个零系数因子 \(0 u^n\),为了排除这种情况,对 \(R[u]\) 中多项式元素的表示进行处理:
首先, 将 \(R[u]\) 中元素写成
\[ f(u)=\sum_{i=0}^{+\infty} a_i u^i \]
其中只有有限个 \(a_i\) 不为 0,因为 \(R[u]\) 中元素必为代数元,所以有确定的次数 \(n=\operatorname{deg}(f(u),R)\),所以当 \(i>n\) 时恒有 \(a_i=0\)
最后可以等价写为一个无穷序列的形式:\((a_0,a_1,\ldots,a_n,0,0,\ldots)\)
注意 \(0=0+0u+\cdots+0u^n\in R[u]\),其称为零多项式,一般可以认为 \(\operatorname{deg}(0,R)=-\infty\)或者零多项式没有次数
一元多项式环的存在性
最后引出重要定理:
可换幺环上的一元多项式环一定存在,即任意可环幺环上都可以定义一元多项式环
证明比较复杂,笔者只能简单写下思路,假设可换幺环为 \(R\):
证明存在大环 \(\widetilde R=\{(a_0,a_1,\ldots,0,0,\ldots)\mid a_i\in R\}\),其中的非零元有限
在 \(\widetilde R\) 中找到一个子环 \(R_0\),使得 \(R_0\cong R\),即两个环同构
在 \(\widetilde R\backslash R_0\) 找到一个元素 \(u\),证明其为 \(R_0\) 上的不定元
在 \(R_0\) 添加上 \(u\) 形成一元多项式环 \(R_0[u]\),实际上可以证明 \(R_0[u]=\widetilde R\)
由于同构,可以得到 \(R[u]\cong R_0[u]\),即 \(R_0[u]\) 就是 \(R\) 上的一元多项式环
里面有一些细节展开描述:
大环上的加法:
类似于平时认知的多项式相加,即对应系数相加即可:
\[ (a_0,a_1,\ldots)+(b_0,b_1,\ldots)=(a_0+b_0,a_1+b_1,\ldots) \]
大环上的乘法:
其实也类似于平时认知的多项式相乘,但是要注意并不是简单的对应元素相乘。
假设乘积结果的元素为 \(c_k\),即 \((a_0,a_1,\ldots)\times(b_0,b_1,\ldots)=(c_0,c_1,\ldots)\),则 \(\begin{aligned}c_k=\sum_{i+j=k}a_ib_j\end{aligned}\)
要证明对加法成交换群,对乘法成可换幺半群,乘法对加法满足分配律,别忘了还要证明两个运算的封闭性
封闭性只用证明结果的非零元有限,即次数有限即可。
加法的零元(单位元):\(\mathbf{0}=(0,0,\ldots)\)
加法的逆元(负元):\(-(a_0,a_1,\ldots)=(-a_0,-a_1,\ldots)\)
乘法的幺元(单位元):\(\mathbf{1}=(1,0,\ldots)\)
证明幺元:
对于任意的 \(\boldsymbol{a}=\left(a_0, \ldots, a_n, 0,0, \ldots\right)\),设 \(\boldsymbol{1} \boldsymbol{a}=\boldsymbol{b}\),则
\[ b_k=\sum_{i=0}^k 1_i a_{k-i}=1_0 a_k+1_1 a_{k-1}+\cdots+1_k a_0=a_k, k\in\{0,1,\ldots,n\} \]
因为 \(1_0=1\),而 \(1_{i \geq 1}=0\)。这就意味着 \(1 \boldsymbol{a}=\boldsymbol{a}\) 恒成立,因此这里定义的 \(\bf 1\) 就是 \(V\) 的幺元
子环 \(R_0\) 的形式为 \(R_0=\{(a,0,0,\ldots)\mid a\in R\}\),可以证明其为 \(\widetilde R\) 的子环
同态映射为 \(\varphi: R\to R_0, \forall a\in R,\varphi(a)=(a,0,\ldots)\in R_0\),可证为环同构映射
不定元取 \(u=(0,1,0,\ldots)\)
根据大环上的乘法,可以得到 \(u^2=(0,0,1,0,\ldots)\),类似 \(u^k=(\overbrace{0,0,\ldots,0}^{k个0},1,0,\ldots)\)
要证明 \(u\) 是 \(R_0\) 上的不定元,需要证明 \(\forall a_0,a_1,\cdots,a_n\in R\),对应 \(R_0\) 中的元素 \((a_0,0,0,\ldots),(a_1,0,0,\ldots),\ldots,(a_n,0,0,\ldots)\),则
\[ \begin{aligned} &(a,0,0,\ldots)\mathbf{1}+(a,0,0,\ldots)u+\cdots+(a,0,0,\ldots)u^n\\ &=(a,0,0,\ldots)(1,0,0,\ldots)+(a,0,0,\ldots)(0,1,0,\ldots)+\cdots+\\ &\quad~(a,0,0,\ldots)(\overbrace{0,0,\ldots,0}^{n个0},1,0,\ldots)\\ &=(a_0,a_1,\ldots,a_n) \end{aligned} \]
若 \((a_0,a_1,\ldots,a_n)=\bf 0\),说明 \(a_0=a_1=\cdots=a_n=0\),即 \(u\) 确实为 \(R_0\) 上的不定元。
极小多项式 Minimal Polynomial
定义在某个域上的代数元 \(u\),它的极小多项式(最小多项式)为满足 \(f(u)=0\) 的 最低次 首一多项式 \(f\)
换句话理解,\(f\) 是该域上次数最小的首一多项式,使得 $ u $ 为 \(f\) 的根
如果 \(u\) 的极小多项式存在,则是唯一的
